深度学习三——深度学习中的数学

线性代数

下面我们将介绍线性代数中的基本数学对象、算术和运算，并用数学符号和相应的代码实现来表示它们。

向量

• [你可以将向量视为标量值组成的列表]。我们将这些标量值称为向量的元素（element）或分量（component）。当我们的向量表示数据集中的样本时，它们的值具有一定的现实意义。例如，如果我们正在训练一个模型来预测贷款违约风险，我们可能会将每个申请人与一个向量相关联，其分量与其收入、工作年限、过往违约次数和其他因素相对应。如果我们正在研究医院患者可能面临的心脏病发作风险，我们可能会用一个向量来表示每个患者，其分量为最近的生命体征、胆固醇水平、每天运动时间等。在数学表示法中，我们通常将向量记为粗体、小写的符号（例如，$\mathbf{x}$、$\mathbf{y}$和$\mathbf{z})$）。
• 我们通过一维张量处理向量。一般来说，张量可以具有任意长度，取决于机器的内存限制。

import tensorflow as tf
x = tf.range(4)
x

<tf.Tensor: shape=(4,), dtype=int32, numpy=array([0, 1, 2, 3], dtype=int32)>

• 我们可以使用下标来引用向量的任一元素。例如，我们可以通过$x_i$来引用第$i$个元素。注意，元素$x_i$是一个标量，所以我们在引用它时不会加粗。大量文献认为列向量是向量的默认方向。在数学中，向量$\mathbf{x}$可以写为：

$\mathbf{x} =\begin{bmatrix}x_{1} \\x_{2} \\ \vdots \\x_{n}\end{bmatrix},$

x[3] #用下标来获取第4个元素值3

<tf.Tensor: shape=(), dtype=int32, numpy=3>

矩阵

• 正如向量将标量从零阶推广到一阶，矩阵将向量从一阶推广到二阶。矩阵，我们通常用粗体、大写字母来表示（例如，$\mathbf{X}$、$\mathbf{Y}$和$\mathbf{Z}$），在代码中表示为具有两个轴的张量。

• 在数学表示法中，我们使用$\mathbf{A} \in \mathbb{R}^{m \times n}$来表示矩阵$\mathbf{A}$，其由$m$行和$n$列的实值标量组成。直观地，我们可以将任意矩阵$\mathbf{A} \in \mathbb{R}^{m \times n}$视为一个表格，其中每个元素$a_{ij}$属于第$i$行第$j$列：

$\mathbf{A}=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix}.$

• 对于任意$\mathbf{A} \in \mathbb{R}^{m \times n}$,$\mathbf{A}$的形状是（$m$,$n$）或$m \times n$。当矩阵具有相同数量的行和列时，其形状将变为正方形；因此，它被称为方矩阵（square matrix）。
• 当调用函数来实例化张量时，我们可以[通过指定两个分量$m$和$n$来创建一个形状为$m \times n$的矩阵]。

A = tf.reshape(tf.range(20), (5, 4))
A

<tf.Tensor: shape=(5, 4), dtype=int32, numpy=
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19]], dtype=int32)>

• 矩阵的转置：有时候，我们想翻转轴。当我们交换矩阵的行和列时，结果称为矩阵的转置（transpose）。我们用$\mathbf{a}^\top$来表示矩阵的转置，如果$\mathbf{B}=\mathbf{A}^\top$，则对于任意$i$和$j$，都有$b_{ij}=a_{ji}$。因此，上面矩阵中的转置是一个形状为$n \times m$的矩阵：

$\mathbf{A}^\top = \begin{bmatrix} a_{11} & a_{21} & \dots & a_{m1} \\ a_{12} & a_{22} & \dots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \dots & a_{mn} \end{bmatrix}.$

• 现在我们在代码中访问(矩阵的转置)。

tf.transpose(A)

<tf.Tensor: shape=(4, 5), dtype=int32, numpy=
array([[ 0,  4,  8, 12, 16],
       [ 1,  5,  9, 13, 17],
       [ 2,  6, 10, 14, 18],
       [ 3,  7, 11, 15, 19]], dtype=int32)>

• 矩阵的作用：矩阵允许我们组织具有不同变化模式的数据。例如，我们矩阵中的行可能对应于不同的房屋（数据样本），而列可能对应于不同的属性。如果你曾经使用过电子表格软件。因此，尽管单个向量的默认方向是列向量，但在表示表格数据集的矩阵中，将每个数据样本作为矩阵中的行向量更为常见。这种约定将支持常见的深度学习实践。

张量

• [就像向量是标量的推广，矩阵是向量的推广一样，我们可以构建具有更多轴的数据结构]。张量（本小节中的“张量”指代数对象）为我们提供了描述具有任意数量轴的$n$维数组的通用方法。例如，向量是一阶张量，矩阵是二阶张量。张量用特殊字体的大写字母（例如，$\mathsf{X}$、$\mathsf{Y}$和$\mathsf{Z}$）表示，它们的索引机制（例如$x_{ijk}$和$[\mathsf{X}]_{1,2i-1,3}$）与矩阵类似。

• 当我们开始处理图像时，张量将变得更加重要，图像以$n$维数组形式出现，其中3个轴对应于高度、宽度，以及一个通道（channel）轴，用于堆叠颜色通道（红色、绿色和蓝色）。

X = tf.reshape(tf.range(24), (2, 3, 4))
X

<tf.Tensor: shape=(2, 3, 4), dtype=int32, numpy=
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]], dtype=int32)>

降维

• 我们可以对任意张量进行的一个有用的操作是[计算其元素的和]。在数学表示法中，我们使用$\sum$符号表示求和。为了表示长度为$d$的向量中元素的总和，可以记为$\sum_{i=1}^dx_i$。在代码中，我们可以调用计算求和的函数：

x = tf.range(4, dtype=tf.float32)
x, tf.reduce_sum(x)

(<tf.Tensor: shape=(4,), dtype=float32, numpy=array([0., 1., 2., 3.], dtype=float32)>,
 <tf.Tensor: shape=(), dtype=float32, numpy=6.0>)

• 我们可以(表示任意形状张量的元素和)。例如，矩阵$\mathbf{A}$中元素的和可以记为$\sum_{i=1}^{m} \sum_{j=1}^{n} a_{ij}$。

A.shape, tf.reduce_sum(A)

(TensorShape([5, 4]), <tf.Tensor: shape=(), dtype=float32, numpy=190.0>)

• 默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。我们还可以[指定张量沿哪一个轴来通过求和降低维度]。
• 以矩阵为例，为了通过求和所有行的元素来降维（轴0），我们可以在调用函数时指定axis=0。由于输入矩阵沿0轴降维以生成输出向量，因此输入的轴0的维数在输出形状中丢失。

A_sum_axis0 = tf.reduce_sum(A, axis=0)
A_sum_axis0, A_sum_axis0.shape

(<tf.Tensor: shape=(4,), dtype=int32, numpy=array([40, 45, 50, 55], dtype=int32)>,
 TensorShape([4]))

• 指定axis=1将通过汇总所有列的元素降维（轴1）。因此，输入的轴1的维数在输出形状中消失。

A_sum_axis1 = tf.reduce_sum(A, axis=1)
A_sum_axis1, A_sum_axis1.shape

(<tf.Tensor: shape=(5,), dtype=float32, numpy=array([ 6., 22., 38., 54., 70.], dtype=float32)>,
 TensorShape([5]))

• 沿着行和列对矩阵求和，等价于对矩阵的所有元素进行求和。

tf.reduce_sum(A, axis=[0, 1])  # Same as `tf.reduce_sum(A)`

<tf.Tensor: shape=(), dtype=int32, numpy=190>

• [一个与求和相关的量是平均值（mean或average）]。我们通过将总和除以元素总数来计算平均值。在代码中，我们可以调用函数来计算任意形状张量的平均值。

tf.reduce_mean(A), tf.reduce_sum(A) / tf.size(A).numpy()

(<tf.Tensor: shape=(), dtype=float32, numpy=9.5>,
 <tf.Tensor: shape=(), dtype=float32, numpy=9.5>)

• 同样，计算平均值的函数也可以沿指定轴降低张量的维度。

tf.reduce_mean(A, axis=0), tf.reduce_sum(A, axis=0) / A.shape[0]

(<tf.Tensor: shape=(4,), dtype=float32, numpy=array([ 8.,  9., 10., 11.], dtype=float32)>,
 <tf.Tensor: shape=(4,), dtype=float32, numpy=array([ 8.,  9., 10., 11.], dtype=float32)>)

非降维求和

• 但是，有时在调用函数来[计算总和或均值时保持轴数不变]会很有用。

sum_A = tf.reduce_sum(A, axis=1, keepdims=True)
sum_A

<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[ 6.],
       [22.],
       [38.],
       [54.],
       [70.]], dtype=float32)>

• 例如，由于sum_A在对每行进行求和后仍保持两个轴，我们可以(通过广播将A除以sum_A)。

A / sum_A

<tf.Tensor: shape=(5, 4), dtype=float32, numpy=
array([[0.        , 0.16666667, 0.33333334, 0.5       ],
       [0.18181819, 0.22727273, 0.27272728, 0.3181818 ],
       [0.21052632, 0.23684211, 0.2631579 , 0.28947368],
       [0.22222222, 0.24074075, 0.25925925, 0.2777778 ],
       [0.22857143, 0.24285714, 0.25714287, 0.27142859]], dtype=float32)>

• 如果我们想沿[某个轴计算A元素的累积总和]，比如axis=0（按行计算），我们可以调用cumsum函数。此函数不会沿任何轴降低输入张量的维度。

tf.cumsum(A, axis=0) # 最后一行是前面的和

<tf.Tensor: shape=(5, 4), dtype=int32, numpy=
array([[ 0,  1,  2,  3],
       [ 4,  6,  8, 10],
       [12, 15, 18, 21],
       [24, 28, 32, 36],
       [40, 45, 50, 55]], dtype=int32)>

点积（Dot Product）

• 到目前为止，我们只执行了按元素操作、求和及平均值。如果这就是我们所能做的，那么线性代数可能就不需要单独一节了。但是，最基本的操作之一是点积。给定两个向量$\mathbf{x},\mathbf{y}\in\mathbb{R}^d$，它们的点积（dotproduct）$\mathbf{x}^\top\mathbf{y}$(转置、相乘再累加)是相同位置的按元素乘积的和：$\mathbf{x}^\top \mathbf{y} = \sum_{i=1}^{d} x_i y_i$。
  • 使用矩阵的tensordot函数进行矩阵乘法。

y = tf.ones(4, dtype=tf.float32)
x, y, tf.tensordot(x, y, axes=1)

(<tf.Tensor: shape=(4,), dtype=float32, numpy=array([0., 1., 2., 3.], dtype=float32)>,
 <tf.Tensor: shape=(4,), dtype=float32, numpy=array([1., 1., 1., 1.], dtype=float32)>,
 <tf.Tensor: shape=(), dtype=float32, numpy=6.0>)

• 注意，(我们可以通过执行按元素乘法，然后进行求和来表示两个向量的点积)：

tf.reduce_sum(x * y)

<tf.Tensor: shape=(), dtype=float32, numpy=6.0>

矩阵-向量积

• 现在我们知道如何计算点积，我们可以开始理解矩阵-向量积（matrix-vector product）。定义矩阵$\mathbf{A} \in \mathbb{R}^{m \times n}$和向量$\mathbf{x} \in \mathbb{R}^n$。让我们将矩阵$\mathbf{A}$用它的行向量表示

$\mathbf{A}= \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_m \\ \end{bmatrix},$

• 其中每个$\mathbf{a}^\top_{i} \in \mathbb{R}^n$都是行向量，表示矩阵的第$i$行。[矩阵向量积$\mathbf{A}\mathbf{x}$是一个长度为$m$的列向量，其第$i$个元素是点积$\mathbf{a}^\top_i \mathbf{x}$]：

$\mathbf{A}\mathbf{x} = \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_m \\ \end{bmatrix}\mathbf{x} = \begin{bmatrix} \mathbf{a}^\top_{1} \mathbf{x} \\ \mathbf{a}^\top_{2} \mathbf{x} \\ \vdots\\ \mathbf{a}^\top_{m} \mathbf{x}\\ \end{bmatrix}.$

• 我们可以把一个矩阵$\mathbf{A} \in \mathbb{R}^{m \times n}$乘法看作是一个从$\mathbb{R}^{n}$到$\mathbb{R}^{m}$向量的转换。这些转换证明是非常有用的。例如，我们可以用方阵的乘法来表示旋转。
• 在代码中使用张量表示矩阵-向量积，我们使用与点积相同的dot函数。当我们为矩阵A和向量x调用np.dot(A,x)时，会执行矩阵-向量积。注意，A的列维数（沿轴1的长度）必须与x的维数（其长度）相同。

x = tf.range(4)
A, x

(<tf.Tensor: shape=(5, 4), dtype=int32, numpy=
 array([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]], dtype=int32)>,
 <tf.Tensor: shape=(4,), dtype=int32, numpy=array([0, 1, 2, 3], dtype=int32)>)

tf.linalg.matvec(A, x) # 计算矩阵A和一维向量x（一维向量是行的方式展示，但实质是列向量）的乘积

<tf.Tensor: shape=(5,), dtype=int32, numpy=array([ 14,  38,  62,  86, 110], dtype=int32)>

矩阵-矩阵乘法

• 假设我们有两个矩阵$\mathbf{A} \in \mathbb{R}^{n \times k}$和$\mathbf{B} \in \mathbb{R}^{k \times m}$：

$\mathbf{A}=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1k} \\ a_{21} & a_{22} & \cdots & a_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nk} \\ \end{bmatrix},\quad \mathbf{B}=\begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1m} \\ b_{21} & b_{22} & \cdots & b_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ b_{k1} & b_{k2} & \cdots & b_{km} \\ \end{bmatrix}.$

• 用行向量$\mathbf{a}^\top_{i} \in \mathbb{R}^k$表示矩阵$\mathbf{A}$的第$i$行，并让列向量$\mathbf{b}_{j} \in \mathbb{R}^k$作为矩阵$\mathbf{B}$的第$j$列。要生成矩阵积$\mathbf{C} = \mathbf{A}\mathbf{B}$，最简单的方法是考虑$\mathbf{A}$的行向量和$\mathbf{B}$的列向量:

$\mathbf{A}= \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_n \\ \end{bmatrix}, \quad \mathbf{B}=\begin{bmatrix} \mathbf{b}_{1} & \mathbf{b}_{2} & \cdots & \mathbf{b}_{m} \\ \end{bmatrix}.$

• 当我们简单地将每个元素$c_{ij}$计算为点积$\mathbf{a}^\top_i \mathbf{b}_j$:

$\mathbf{C} = \mathbf{AB} = \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_n \\ \end{bmatrix} \begin{bmatrix} \mathbf{b}_{1} & \mathbf{b}_{2} & \cdots & \mathbf{b}_{m} \\ \end{bmatrix} = \begin{bmatrix} \mathbf{a}^\top_{1} \mathbf{b}_1 & \mathbf{a}^\top_{1}\mathbf{b}_2& \cdots & \mathbf{a}^\top_{1} \mathbf{b}_m \\ \mathbf{a}^\top_{2}\mathbf{b}_1 & \mathbf{a}^\top_{2} \mathbf{b}_2 & \cdots & \mathbf{a}^\top_{2} \mathbf{b}_m \\ \vdots & \vdots & \ddots &\vdots\\ \mathbf{a}^\top_{n} \mathbf{b}_1 & \mathbf{a}^\top_{n}\mathbf{b}_2& \cdots& \mathbf{a}^\top_{n} \mathbf{b}_m \end{bmatrix}.$

• [我们可以将矩阵-矩阵乘法$\mathbf{AB}$看作是简单地执行$m$次矩阵-向量积，并将结果拼接在一起，形成一个$n \times m$矩阵]。在下面的代码中，我们在A和B上执行矩阵乘法。这里的A是一个5行4列的矩阵，B是一个4行3列的矩阵。相乘后，我们得到了一个5行3列的矩阵。

B = tf.ones((4, 3), dtype=tf.int32)
C = tf.matmul(A, B)
A, B, C

(<tf.Tensor: shape=(5, 4), dtype=int32, numpy=
 array([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]], dtype=int32)>,
 <tf.Tensor: shape=(4, 3), dtype=int32, numpy=
 array([[1, 1, 1],
        [1, 1, 1],
        [1, 1, 1],
        [1, 1, 1]], dtype=int32)>,
 <tf.Tensor: shape=(5, 3), dtype=int32, numpy=
 array([[ 6,  6,  6],
        [22, 22, 22],
        [38, 38, 38],
        [54, 54, 54],
        [70, 70, 70]], dtype=int32)>)

• 矩阵-矩阵乘法可以简单地称为矩阵乘法，不应与元素分别对应相乘混淆。

范数

• 在线性代数中，向量范数是将向量映射到标量的函数$f$。向量范数要满足一些属性。
• 给定任意向量$\mathbf{x}$，第一个性质说，如果我们按常数因子$\alpha$缩放向量的所有元素，其范数也会按相同常数因子的绝对值缩放：

$f(\alpha \mathbf{x}) = |\alpha| f(\mathbf{x}).$

• 第二个性质是我们熟悉的三角不等式:

$f(\mathbf{x} + \mathbf{y}) \leq f(\mathbf{x}) + f(\mathbf{y}).$

• 第三个性质简单地说范数必须是非负的:

$f(\mathbf{x}) \geq 0.$

• 最后一个性质要求范数最小为0，当且仅当向量全由0组成。

$\forall i, [\mathbf{x}]_i = 0 \Leftrightarrow f(\mathbf{x})=0.$

• $L_2$范数：欧几里得距离（两点之间的距离）是一个范数：具体而言，它是$L_2$范数。假设$n$维向量$\mathbf{x}$中的元素是$x_1,\ldots,x_n$，其[$L_2$范数是向量元素平方和的平方根：]

  $\|\mathbf{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2},$

• 其中，在$L_2$范数中常常省略下标$2$，也就是说，$\|\mathbf{x}\|$等同于$\|\mathbf{x}\|_2$。在代码中，我们可以按如下方式计算向量的$L_2$范数。

u = tf.constant([3.0, -4.0])
tf.norm(u) # 勾股定理3， 4， 5

<tf.Tensor: shape=(), dtype=float32, numpy=5.0>

• $L_1$范数：在深度学习中，我们更经常地使用$L_2$范数的平方。你还会经常遇到[$L_1$范数，它表示为向量元素的绝对值之和.与$L_2$范数相比，$L_1$范数受异常值的影响较小.

  $\|\mathbf{x}\|_1 = \sum_{i=1}^n \left|x_i \right|.$

• 为了计算$L_1$范数，我们将绝对值函数和按元素求和组合起来。

a = tf.abs(u)
b = tf.reduce_sum(a) # 按0轴求和
b

<tf.Tensor: shape=(), dtype=float32, numpy=7.0>

• $L_p$范数: $L_2$范数和$L_1$范数都是更一般的$L_p$范数的特例：

$\|\mathbf{x}\|_p = \left(\sum_{i=1}^n \left|x_i \right|^p \right)^{1/p}.$

• 弗罗贝尼乌斯范数: 类似于向量的$L_2$范数，[矩阵]$\mathbf{X} \in \mathbb{R}^{m \times n}$(的弗罗贝尼乌斯范数（Frobenius norm）是矩阵元素平方和的平方根：)

  $\|\mathbf{X}\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n x_{ij}^2}.$

• 弗罗贝尼乌斯范数满足向量范数的所有性质，它就像是矩阵形向量的$L_2$范数。调用norm函数将计算矩阵的弗罗贝尼乌斯范数。

tf.norm(tf.ones((4, 9))) # 每个元素都为1，有36个1，36个1的平方为36再开方为6

<tf.Tensor: shape=(), dtype=float32, numpy=6.0>

微分

导数和微分

• 导数概念：假设我们有一个函数$f: \mathbb{R}^n \rightarrow \mathbb{R}$，其输入和输出都是标量。($f$的导数被定义为)

($$f’(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h},$$)

• 如果这个极限存在。如果$f'(a)$存在，则称$f$在$a$处是可微（differentiable）的。如果$f$在一个区间内的每个数上都是可微的，则此函数在此区间中是可微的。我们可以将$f'(x)$解释为$f(x)$相对于$x$的瞬时（instantaneous）变化率。所谓的瞬时变化率是基于$x$中的变化$h$，且$h$接近$0$。

• 为了更好地解释导数，让我们用一个例子来做实验。(定义$u=f(x)=3x^2-4x$.)

%matplotlib inline
import numpy as np
from IPython import display
import tensorflow as tf
from matplotlib import pyplot as plt

# 定义基础函数
def f(x):
    return 3 * x ** 2 - 4 * x

• [通过令$x=1$并让$h$接近$0$，], ($\frac{f(x+h)-f(x)}{h}$的数值结果接近$2$，函数在1处的导数值)。虽然这个实验不是一个数学证明，但我们稍后会看到，当$x=1$时，导数$u'$是$2$。

# 定义计算变化率的函数
def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h

h = 0.1
for i in range(5):
    print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
    h *= 0.1

h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003

• 计算$u'=f'(x)=3\frac{d}{dx}x^2-4\frac{d}{dx}x=6x-4$。因此，通过令$x=1$，我们有$u'=2$：这一点得到了我们在本节前面的实验的支持，在这个实验中，数值结果接近$2$。当$x=1$时，此导数也是曲线$u=f(x)$切线的斜率。

• [为了对导数的这种解释进行可视化，]我们将使用matplotlib，这是一个Python中流行的绘图库。要配置matplotlib生成图形的属性，我们需要(定义几个函数)。

  • 在下面，use_svg_display函数指定matplotlib软件包输出svg图表以获得更清晰的图像。

def use_svg_display():  
    """使用svg格式在Jupyter中显示绘图。"""
    display.set_matplotlib_formats('svg')

• 我们定义set_figsize函数来设置图表大小。

def set_figsize(figsize=(3.5, 2.5)):  
    """设置matplotlib的图表大小。"""
    use_svg_display()
    plt.rcParams['figure.figsize'] = figsize

• 下面的set_axes函数用于设置由matplotlib生成图表的轴的属性。

def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """设置matplotlib的轴。"""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()

• 通过这三个用于图形配置的函数，我们定义了plot函数来简洁地绘制多条曲线。

def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """绘制数据点。"""
    if legend is None:
        legend = []

    set_figsize(figsize)
    axes = axes if axes else plt.gca()

    # 如果 `X` 有一个轴，输出True
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))

    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)

• 现在我们可以[绘制函数$u=f(x)$及其在$x=1$处的切线$y=2x-3$]，其中系数$2$是切线的斜率。

x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])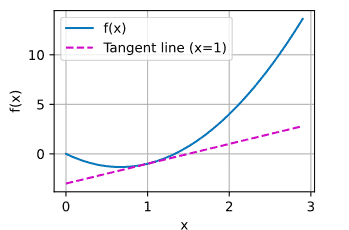

偏导数

在深度学习中，函数通常依赖于许多变量。因此，我们需要将微分的思想推广到这些多元函数（multivariate function）上。

设$y = f(x_1, x_2, \ldots, x_n)$是一个具有$n$个变量的函数。$y$关于第$i$个参数$x_i$的偏导数（partial derivative）为：

$\frac{\partial y}{\partial x_i} = \lim_{h \rightarrow 0} \frac{f(x_1, \ldots, x_{i-1}, x_i+h, x_{i+1}, \ldots, x_n) - f(x_1, \ldots, x_i, \ldots, x_n)}{h}.$

为了计算$\frac{\partial y}{\partial x_i}$，我们可以简单地将$x_1, \ldots, x_{i-1}, x_{i+1}, \ldots, x_n$看作常数，并计算$y$关于$x_i$的导数。对于偏导数的表示，以下是等价的：

$\frac{\partial y}{\partial x_i} = \frac{\partial f}{\partial x_i} = f_{x_i} = f_i = D_i f = D_{x_i} f.$

梯度

我们可以连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量。设函数$f:\mathbb{R}^n\rightarrow\mathbb{R}$的输入是一个$n$维向量$\mathbf{x}=[x_1,x_2,\ldots,x_n]^\top$，并且输出是一个标量。
函数$f(\mathbf{x})$相对于$\mathbf{x}$的梯度是一个包含$n$个偏导数的向量:

$\nabla_{\mathbf{x}} f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_n}\bigg]^\top,$

其中$\nabla_{\mathbf{x}} f(\mathbf{x})$通常在没有歧义时被$\nabla f(\mathbf{x})$取代。

同样，对于任何矩阵$\mathbf{X}$，我们都有$\nabla_{\mathbf{X}} \|\mathbf{X} \|_F^2 = 2\mathbf{X}$。正如我们之后将看到的，梯度对于设计深度学习中的优化算法有很大用处。

链式法则

然而，上面方法可能很难找到梯度。
这是因为在深度学习中，多元函数通常是复合（composite）的，所以我们可能没法应用上述任何规则来微分这些函数。
幸运的是，链式法则使我们能够微分复合函数。

让我们先考虑单变量函数。假设函数$y=f(u)$和$u=g(x)$都是可微的，根据链式法则：

$\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}.$

现在让我们把注意力转向一个更一般的场景，即函数具有任意数量的变量的情况。假设可微分函数$y$有变量$u_1, u_2, \ldots, u_m$，其中每个可微分函数$u_i$都有变量$x_1, x_2, \ldots, x_n$。注意，$y$是$x_1, x_2， \ldots, x_n$的函数。对于任意$i = 1, 2, \ldots, n$，链式法则给出：

$\frac{dy}{dx_i} = \frac{dy}{du_1} \frac{du_1}{dx_i} + \frac{dy}{du_2} \frac{du_2}{dx_i} + \cdots + \frac{dy}{du_m} \frac{du_m}{dx_i}$

自动求导

• 深度学习框架通过自动计算导数，即自动求导（automatic differentiation），来加快这项工作。实际中，根据我们设计的模型，系统会构建一个计算图（computational graph），来跟踪计算是哪些数据通过哪些操作组合起来产生输出。自动求导使系统能够随后反向传播梯度。这里，反向传播（backpropagate）只是意味着跟踪整个计算图，填充关于每个参数的偏导数。

标量变量的反向传播

作为一个演示例子，(假设我们想对函数$y=2\mathbf{x}^{\top}\mathbf{x}$关于列向量$\mathbf{x}$求导)。首先，我们创建变量x并为其分配一个初始值。

import tensorflow as tf

x = tf.range(4, dtype=tf.float32)
x

<tf.Tensor: shape=(4,), dtype=float32, numpy=array([0., 1., 2., 3.], dtype=float32)>

[在我们计算$y$关于$\mathbf{x}$的梯度之前，我们需要一个地方来存储梯度。]
重要的是，我们不会在每次对一个参数求导时都分配新的内存。因为我们经常会成千上万次地更新相同的参数，每次都分配新的内存可能很快就会将内存耗尽。注意，标量函数关于向量$\mathbf{x}$的梯度是向量，并且与$\mathbf{x}$具有相同的形状。

x = tf.Variable(x) # Variable是持久存储的特殊张量

(现在让我们计算$y$。)

# 把所有计算记录在磁带上(实质是一个上下文管理器，自动监测Variable变量)
with tf.GradientTape() as t:
    y = 2 * tf.tensordot(x, x, axes=1) # 计算x的内积，实质就是X的转置和X相乘，得出y
y

<tf.Tensor: shape=(), dtype=float32, numpy=28.0>

x是一个长度为4的向量，计算x和x的内积，得到了我们赋值给y的标量输出。接下来，我们可以[通过调用反向传播函数来自动计算y关于x每个分量的梯度]，并打印这些梯度。

x_grad = t.gradient(y, x) # 方向传播函数求y关于x每个分量的梯度
x_grad

<tf.Tensor: shape=(4,), dtype=float32, numpy=array([ 0.,  4.,  8., 12.], dtype=float32)>

函数$y=2\mathbf{x}^{\top}\mathbf{x}$关于$\mathbf{x}$的梯度应为$4\mathbf{x}$。让我们快速验证我们想要的梯度是否正确计算。

x_grad == 4 * x

<tf.Tensor: shape=(4,), dtype=bool, numpy=array([ True,  True,  True,  True])>

[现在让我们计算x的另一个函数。]

with tf.GradientTape() as t:
    y = tf.reduce_sum(x) #将所有元素求和得到结果赋值给y
t.gradient(y, x)  # 因为有上下文管理器，所以上次计算的梯度被保存，重新调用会使原来的梯度被新计算的梯度覆盖

<tf.Tensor: shape=(4,), dtype=float32, numpy=array([1., 1., 1., 1.], dtype=float32)>

非标量变量的反向传播

当y不是标量时，向量y关于向量x的导数的最自然解释是一个矩阵。对于高阶和高维的y和x，求导的结果可以是一个高阶张量。

然而，虽然这些更奇特的对象确实出现在高级机器学习中（包括[深度学习中]），但当我们调用向量的反向计算时，我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。这里(，我们的目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和。)

with tf.GradientTape() as t:
    y = x * x
x, y# y是一个向量

(<tf.Variable 'Variable:0' shape=(4,) dtype=float32, numpy=array([0., 1., 2., 3.], dtype=float32)>,
 <tf.Tensor: shape=(4,), dtype=float32, numpy=array([0., 1., 4., 9.], dtype=float32)>)

# 反向传播，计算梯度
#t.gradient(y, x)  # 等价于 `y = tf.reduce_sum(x * x)`
y = tf.reduce_sum(x * x)
y

<tf.Tensor: shape=(), dtype=float32, numpy=14.0>

分离计算

有时，我们希望[将某些计算移动到记录的计算图之外]。
例如，假设y是作为x的函数计算的，而z则是作为y和x的函数计算的。
现在，想象一下，我们想计算z关于x的梯度，但由于某种原因，我们希望将y视为一个常数，并且只考虑到x在y被计算后发挥的作用。

在这里，我们可以分离y来返回一个新变量u，该变量与y具有相同的值，但丢弃计算图中如何计算y的任何信息。换句话说，梯度不会向后流经u到x。因此，下面的反向传播函数计算z=u*x关于x的偏导数，同时将u作为常数处理，而不是z=x*x*x关于x的偏导数。

# 设置 `persistent=True` 来运行 `t.gradient`多次
with tf.GradientTape(persistent=True) as t:
    y = x * x
    u = tf.stop_gradient(y)
    z = u * x

x_grad = t.gradient(z, x)
x_grad == u

<tf.Tensor: shape=(4,), dtype=bool, numpy=array([ True,  True,  True,  True])>

由于记录了y的计算结果，我们可以随后在y上调用反向传播，得到y=x*x关于的x的导数，这里是2*x。

t.gradient(y, x) == 2 * x

<tf.Tensor: shape=(4,), dtype=bool, numpy=array([ True,  True,  True,  True])>

Python控制流的梯度计算

使用自动求导的一个好处是，[即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度]。在下面的代码中，while循环的迭代次数和if语句的结果都取决于输入a的值。

def f(a):
    b = a * 2
    while tf.norm(b) < 1000:
        b = b * 2
    if tf.reduce_sum(b) > 0:
        c = b
    else:
        c = 100 * b
    return c

让我们计算梯度。

a = tf.Variable(tf.random.normal(shape=()))
with tf.GradientTape() as t:
    d = f(a)
d_grad = t.gradient(d, a)
d_grad

<tf.Tensor: shape=(), dtype=float32, numpy=204800.0>

我们现在可以分析上面定义的f函数。请注意，它在其输入a中是分段线性的。换言之，对于任何a，存在某个常量标量k，使得f(a)=k*a，其中k的值取决于输入a。因此，d/a允许我们验证梯度是否正确。

d_grad == d / a

<tf.Tensor: shape=(), dtype=bool, numpy=True>

概率

编程中的概率论

首先，让我们导入必要的软件包。

import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp

接下来，我们将希望能够投掷骰子。在统计学中，我们把从概率分布中抽取样本的过程称为抽样（sampling）。
将概率分配给一些离散选择的分布称为多项分布（multinomial distribution）。稍后我们将给出分布（distribution）的更正式定义。

为了抽取一个样本，我们只需传入一个概率向量。
输出是另一个相同长度的向量：它在索引$i$处的值是采样结果中$i$出现的次数，由采样函数模拟真实情况分配。

fair_probs = tf.ones(6) / 6 # 概率向量，每一个元素代表一个事件，值为这个事件的真实概率
tfp.distributions.Multinomial(1, fair_probs).sample() # 该函数模拟真实情况对6个事件进行采样结果分配（传入的6个元素的向量）
# 参数1表示只抽取一次样本

<tf.Tensor: shape=(6,), dtype=float32, numpy=array([0., 0., 0., 0., 1., 0.], dtype=float32)>

同时抽取多个样本: 如果你运行采样器很多次，你会发现每次你都得到随机的值。在估计一个骰子的公平性时，我们经常希望从同一分布中生成多个样本。如果用Python的for循环来完成这个任务，速度会慢得令人难以忍受，因此我们使用的函数支持同时抽取多个样本，返回我们想要的任意形状的独立样本数组。

tfp.distributions.Multinomial(10, fair_probs).sample() # 参数10表示一次抽取10个样本

<tf.Tensor: shape=(6,), dtype=float32, numpy=array([1., 1., 1., 0., 4., 3.], dtype=float32)>

现在我们知道如何对骰子进行采样，我们可以模拟1000次投掷。然后，我们可以统计1000次投掷后,每个数字被投中了多少次。具体来说，我们计算相对频率作为真实概率的估计。

counts = tfp.distributions.Multinomial(1000, fair_probs).sample()
counts / 1000 #根据频率计算概率

<tf.Tensor: shape=(6,), dtype=float32, numpy=array([0.149, 0.17 , 0.175, 0.179, 0.158, 0.169], dtype=float32)>

因为我们是从一个公平的骰子中生成的数据，我们知道每个结果都有真实的概率$\frac{1}{6}$，大约是$0.167$，所以上面输出的估计值看起来不错。

概率论基本原理

条件概率

这给我们带来了一个有趣的比率：
$0 \leq \frac{P(A=a, B=b)}{P(A=a)} \leq 1$。我们称这个比率为条件概率（conditional probability），并用$P(B=b \mid A=a)$表示它：它是$B=b$的概率，前提是$A=a$已发生。

贝叶斯定理

使用条件概率的定义，我们可以得出统计学中最有用和最著名的方程之一：Bayes定理（Bayes’ theorem）。它如下所示。通过构造，我们有乘法规则，$P(A, B) = P(B \mid A) P(A)$。根据对称性，这也适用于$P(A, B) = P(A \mid B) P(B)$。假设$P(B)>0$，求解其中一个条件变量，我们得到

$P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)}.$

请注意，在这里我们使用更紧凑的表示法，其中$P(A, B)$是一个联合分布，$P(A \mid B)$是一个条件分布。这种分布可以在给定值$A = a, B=b$上进行求值。

边际化

如果我们想从另一件事中推断一件事，但我们只知道相反方向的属性，比如因和果的时候，Bayes定理是非常有用的，正如我们将在本节后面看到的那样。为了能进行这项工作，我们需要的一个重要操作是边际化。这项操作是从$P(A, B)$中确定$P(B)$的操作。我们可以看到，$B$的概率相当于计算$A$的所有可能选择，并将所有选择的联合概率聚合在一起：

$P(B) = \sum_{A} P(A, B),$

这也称为求和规则。边际化结果的概率或分布称为边际概率或边际分布。

独立性

另一个要检查的有用属性是依赖与独立。两个随机变量$A$和$B$是独立的，意味着事件$A$的发生不会透露有关$B$事件的发生情况的任何信息。在这种情况下，统计学家通常将这一点表述为$A \perp B$。根据贝叶斯定理，马上就能同样得到$P(A \mid B) = P(A)$。在所有其他情况下，我们称$A$和$B$依赖。比如，一个骰子的两次连续抛出是独立的。相比之下，灯开关的位置和房间的亮度并不是（尽管它们不是具有确定性的，因为总是可能存在灯泡坏掉，电源故障，或者开关故障）。

由于$P(A \mid B) = \frac{P(A, B)}{P(B)} = P(A)$等价于$P(A, B) = P(A)P(B)$，因此两个随机变量是独立的当且仅当两个随机变量的联合分布是其各自分布的乘积。同样地，给定另一个随机变量$C$时，两个随机变量$A$和$B$是条件独立的，当且仅当$P(A, B \mid C) = P(A \mid C)P(B \mid C)$。这个情况表示为$A \perp B \mid C$。

期望和差异

为了概括概率分布的关键特征，我们需要一些测量方法。随机变量$X$的期望（或平均值）表示为

$E[X] = \sum_{x} x P(X = x).$

当函数$f(x)$的输入是从分布$P$中抽取的随机变量时，$f(x)$的期望值为

$E_{x \sim P}[f(x)] = \sum_x f(x) P(x).$

在许多情况下，我们希望衡量随机变量$X$与其期望值的偏置。这可以通过方差来量化

$\mathrm{Var}[X] = E\left[(X - E[X])^2\right] = E[X^2] - E[X]^2.$

它的平方根被称为标准差（standared deviation）。随机变量函数的方差衡量的是，当从该随机变量分布中采样不同值$x$时，函数值偏离该函数的期望的程度：

$\mathrm{Var}[f(x)] = E\left[\left(f(x) - E[f(x)]\right)^2\right].$